Интересные факты о математике

По какой причине математик Григорий Перельман отказался от награды в миллион долларов?
Из семи математических проблем, известных как Задачи тысячелетия, решена только одна — гипотеза Пуанкаре. За её доказательство Математический институт Клэя присудил Григорию Перельману награду размером в миллион долларов. Тот отказался её получать, указав одной из причин то, что награда обошла стороной его коллегу Ричарда Гамильтона, также внёсшего значительный вклад в решение проблемы. В свою очередь, за разработку математической теории, от которой отталкивался Перельман, Гамильтон не отказался от вручаемой в Гонконге Премии Шао, разделив миллион долларов с Димитриосом Христодулу.

В какой стране нельзя победить в промо-конкурсе без решения математического примера?
Канадские законы допускают проведение игр на чистую удачу для лицензированных казино, благотворительных мероприятий и официальных лотерей провинций. В конкурсах, проводимых коммерческим организациями, задания должны проверять конкретные навыки участников либо иметь смешанный формат. На практике участники таких розыгрышей решают в билете математический пример типа (16 × 5) – (12 ÷ 4). Задачки не сводятся к «дважды два» из-за решения суда, согласно которому пример квалифицируется как оценивающий навык, если в нём присутствует не меньше трёх разных действий.
Источник: Wikipedia / Skill testing question

Почему доказавший Великую теорему Ферма учёный получил не золотую Филдсовскую медаль, а серебряный значок?
Престижная Филдсовская премия по математике вручается только учёным не старше 40 лет. Эндрю Уайлсу в 1993 году было как раз 40, когда он представил на конференции доклад о доказательстве Великой теоремы Ферма, которое математики искали более трёхсот лет. Однако вскоре в его выкладках были обнаружены некоторые несоответствия, разрешение которых заняло ещё один год, и только в 1995 году доказательство было опубликовано в журнале «Annals of Mathematics». Претендовать на Филдсовскую золотую медаль Уайлс уже не мог — тем не менее, в знак признательности оргкомитет премии изготовил для него специальный серебряный значок, единственный в своём роде.
Источник: Wikipedia / Fields Medal

Какие функции у слепых может выполнять часть мозга, ответственная за обработку визуальной информации
Часть мозга, ответственная главным образом за обработку визуальной информации, называется зрительной корой. У слепых эта область не отмирает, а переключается на другие функции. В одном исследовании нейрофизиологи обнаружили, что зрительная кора у слепых активируется в процессе распознавания речи, в другом — что она задействуется при решении математических задач.
Источник: N + 1 / Зрительная кора головного мозга слепых людей занялась обработкой речи, Научная Россия / Слепые используют зрительную кору мозга для работы с числами

Какой фигурой можно замостить пространство непериодичным способом?
Долгое время оставалась нерешённой задача одной плитки — геометрическая проблема нахождения фигуры, которой можно замостить пространство, причём непериодичным способом. Решение нашёл в 2022 году математик-любитель Дэвид Смит. Предложенная им фигура, прозванная «шляпой», состоит из восьми склеенных дельтоидов — четырёхугольников, у которых по две смежные стороны равны. Через некоторое время Смит с коллегами оптимизировали решение: если в предыдущем случае некоторые «шляпы» приходилось зеркально отражать, то похожая фигура-«привидение» обеспечивает замощение с использованием только её поворотов.
Источник: Википедия / Задача одной плитки

Кто хотел доказать логическое противоречие в американской конституции на слушании о получении гражданства США?
Австрийский математик Курт Гёдель, известный формулировкой логических теорем о неполноте и их доказательствами, после начала Второй Мировой войны эмигрировал в США. В 1947 году он подал заявку на получение гражданства, и в ходе слушания судья спросил у него, какой был тип правительства в Австрии. Гёдель сказал, что сначала Австрия была республикой, однако из-за несовершенства конституции скатилась в диктатуру. На реплику судьи, что в Америке такое невозможно, Гёдель ответил: «Ещё как возможно, и я могу доказать это прямо здесь», однако судья увёл разговор в другую сторону. Впоследствии, однако, Гёдель не писал и не рассказывал, в чём именно заключается логическая ошибка американской конституции.
Источник: Wikipedia / Gödel's Loophole

Могут ли увеличиться средние значения двух множеств при перемещении элемента из одного множества в другое?
При перемещении элемента из одного множества в другое средние значения обоих множеств могут увеличиться, хотя это кажется контринтуитивным. Данный парадокс назвали феноменом Уилла Роджерса в честь американского комика за его шутку: «Жители Оклахомы, переехавшие в Калифорнию, повысили средний интеллект обоих штатов», подразумевающую, что средний IQ переселенцев был ниже, чем в целом у оклахомцев, но выше, чем у калифорнийцев. Отражение феномена в реальной жизни можно рассмотреть на примере улучшения методов диагностики рака. Благодаря ему люди с выявленными опухолями, которые ещё не причиняют беспокойства, переходят из группы «здоровые» в группу «больные». Как следствие, средняя продолжительность жизни в обеих группах увеличивается.
Источник: Википедия / Феномен Уилла Роджерса

Что стало причиной сотрудничества математиков Кокса и Цукера?
Когда аспиранты Принстонского университета Дэвид Кокс и Стивен Цукер познакомились друг с другом, они решили, что непременно должны написать совместную статью, ведь стоящие рядом фамилии совпадают с непристойностью (Cox-Zucker и «cocksucker»). Итогом их сотрудничества стал алгоритм в области алгебраических поверхностей, известный как машина Кокса-Цукера.
Источник: Википедия / Машина Кокса-Цукера

Какая математическая теорема была впервые доказана в эпизоде мультсериала?
По сюжету 10 эпизода 7 сезона «Футурамы» профессор Фарнсворт с Эми изобрели машину для обмена разумами, и герои начали переселяться в чужие тела. Постепенно всё запуталось, и к концу серии все захотели вернуться в свои тела обратно — тогда на помощь пришли баскетболисты «Гарлем Глобтроттерс», которые математически обосновали, что для этой операции требуются два запасных организма. Автор сценария Кен Килер, обладатель учёной степени по математике, специально для этого эпизода сформулировал теорему в области теории групп, доказательство которой и было представлено на экране.
Источник: Wikipedia / The Prisoner of Benda
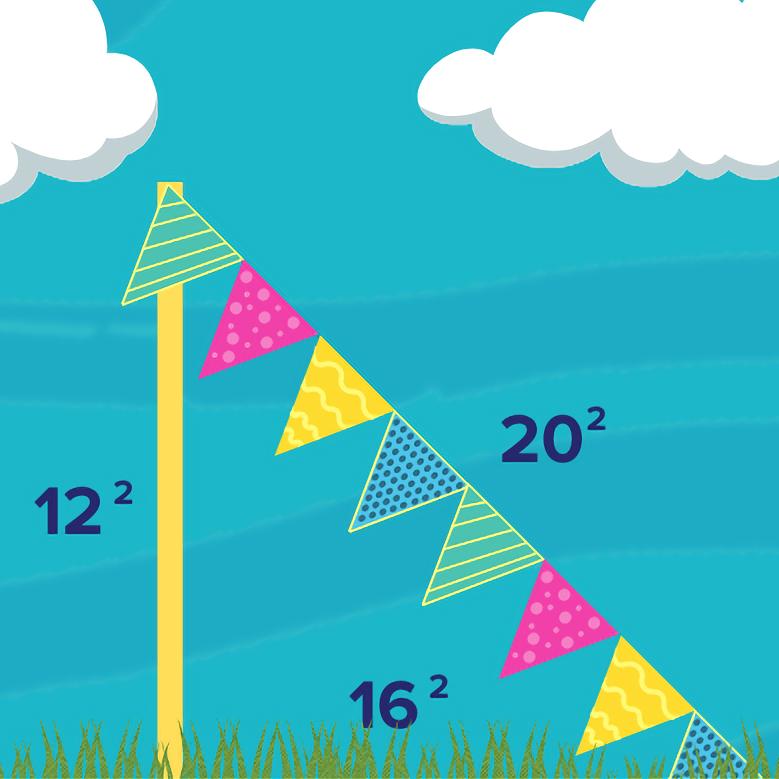
Когда празднуют день теоремы Пифагора?
Время от времени математики празднуют день теоремы Пифагора. Регулярности в праздниках нет, а дата выбирается так, чтобы сумма квадратов числа и номера месяца равнялась квадрату двух последних цифр года. Последний раз праздник выпал на 16 декабря 2020 года (16² + 12² = 20²), а следующий придётся на 24 июля 2025 года.
Источник: Дальневосточный федеральный университет / Математический праздник в честь теоремы Пифагора
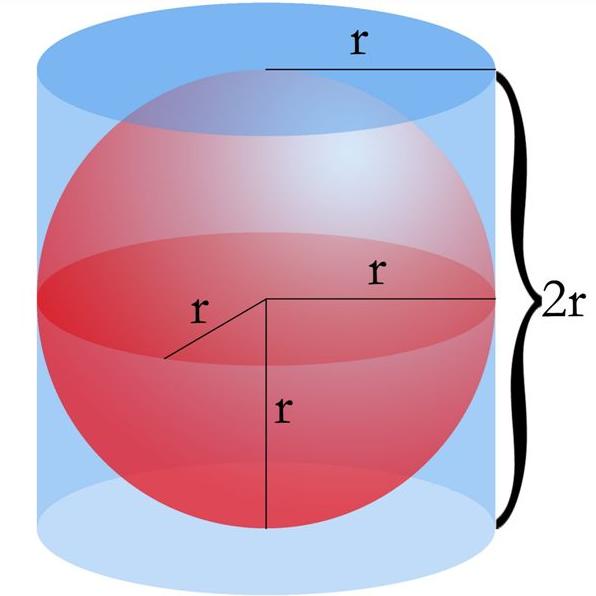
Каким своим открытием больше всего гордился Архимед?
Самым важным своим достижением Архимед считал не названный его именем закон гидростатики и не устройства, которые помогли победить осадивших Сиракузы римлян. Больше всего он гордился открытием того, что объёмы шара и описанного вокруг него цилиндра соотносятся как 2:3. Архимед даже завещал поместить на его могиле скульптуру из вписанного в цилиндр шара, которую упомянул посетивший Сиракузы два века спустя Цицерон.
Источник: Wikipedia / Archimedes
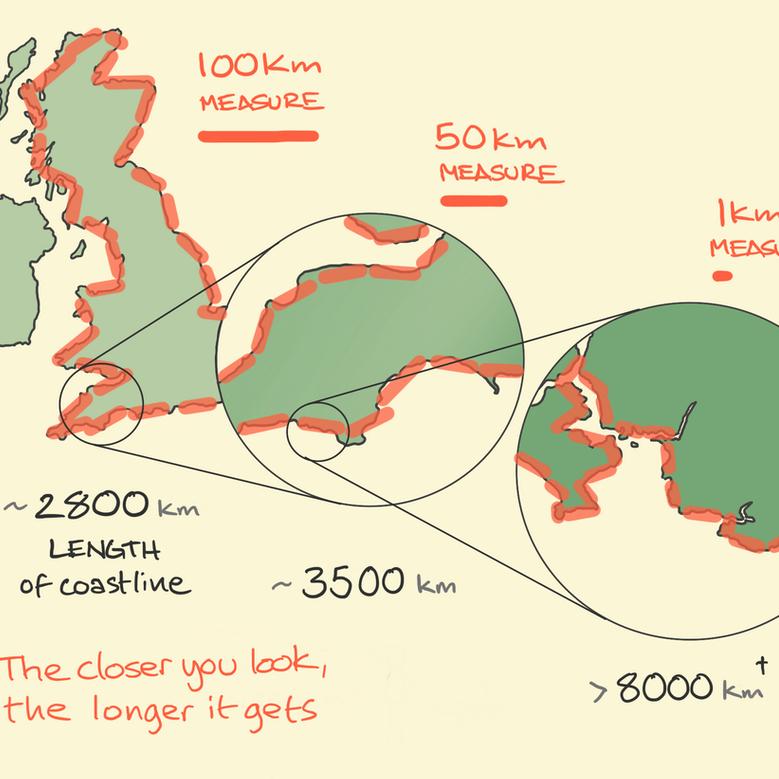
Почему нельзя точно измерить береговую линию?
Парадоксом береговой линии называют невозможность точного измерения кривых на картах — будь то береговая линия или граница между территориями. Для такого измерения нужно выбрать масштаб и аппроксимировать кривую, то есть соединить её точки прямыми отрезками равной длины (например, один километр). Однако изгибы рельефа встречаются на любом масштабе, и чем меньше размер отрезка, тем больше будет итоговая длина, а при спускании на атомарный уровень измерений эта длина будет стремиться к бесконечности. Поэтому в разных справочниках, где есть таблицы ранжирования государств по длине береговой линии, эти длины и порядок ранжирования могут кардинально отличаться друг от друга как раз по причине выбора масштаба, хотя на первом месте неизменно располагается Канада.
Источник: Википедия / Парадокс береговой линии, Википедия / Список стран по длине береговой линии

Какой закон делает невозможным существование гигантских монстров типа Кинг-Конга?
Согласно закону квадрата — куба, при пропорциональном увеличении объекта его объём возрастает пропорционально кубу масштабирующего коэффициента, а площадь поверхности — пропорционально квадрату этого коэффициента. Применительно к живым существам отсюда вытекает принципиальное отличие в скелете и мускулатуре сильно отличающихся размерами животных. Если произвольное животное увеличить, к примеру, в 10 раз, его вес возрастёт сразу в 1000 раз, а вот поперечное сечение костей и мышц — лишь в 100 раз, поэтому скелет попросту не выдержит нагрузку, к тому же не сможет функционировать дыхательная система. Следовательно, вымышленные гигантские насекомые или монстры типа Кинг-Конга, механически отмасштабированные без учёта закона квадрата — куба, не смогли бы существовать.
Источник: Wikipedia / Square–cube law

Для какого языка обычные школьники придумали более эффективную систему записи цифр?
В эскимосско-алеутских языках традиционно сложилась двадцатеричная система исчисления с пятеричной базой, то есть промежуточными отсчётами в точках 5, 10 и 15. В 1994 году, отметив невозможность арифметических операций над их врождёнными представлениями о числах с использованием арабских цифр, группа учеников города Кактовик на Аляске под руководством учителя разработала систему записи цифр от 0 до 19. Полученные символы легко пишутся без отрыва карандаша от бумаги и легко запоминаются. Но самое важное их свойство в упрощении обучения арифметике, так как сложение и вычитание таких цифр зачастую сводится к графическому дописыванию или стиранию нескольких штрихов. Через несколько лет внедрения таких цифр в школьную программу Кактовика параллельно с привычными арабскими резко увеличилась средняя успеваемость по математике, а сейчас они довольно широко распространены и среди взрослых инупиатов.
Источник: Википедия / Кактовикские цифры

Какие насекомые понимают идею чисел, в том числе нуля?
Понимание идеи нуля и размещение его в начале числового ряда присущи не только человеку: в разных экспериментах эта способность выявлялась у макак-резусов, шимпанзе, знаменитого попугая Алекса, а также пчёл. Последних с помощью специальной установки обучали концепциям «больше» и «меньше», используя для подкрепления сахарный сироп и горький хинин в качестве положительного и отрицательного стимулов соответственно. Пройдя подготовку на картинках с количеством фигур от 1 до 4, пчёлы успешно экстраполировали полученные знания на числа 0 и 5. Другая группа пчёл, обучаясь на числах от 2 до 5, всё равно демонстрировала понимание того, что 0 меньше 1.
Какой математический алгоритм помог спасти больше пациентов, нуждающихся в трансплантации?
В экономике для решения задачи о марьяже, то есть нахождения стабильных сочетаний пар, известен алгоритм Гэйла — Шепли, изначально описанный этими учёными на примере формирования брачных союзов. Если взять одинаковое число мужчин и женщин и попросить их составить список предпочтений противоположного пола по убыванию, то алгоритм всегда составит такое распределение пар, чтобы в разных парах не нашлось двух человек, предпочитающих друг друга их назначенным партнёрам, то есть все браки в конечном итоге стабильны. Применение алгоритму нашлось в самых разных областях, например, для назначения новых докторов в больницы или нахождения оптимальных приёмных родителей для сирот. А экономист Элвин Рот использовал его в США для изменения системы распределения донорских почек, что на порядок увеличило количество спасённых реципиентов. Проблема была в том, что люди часто готовы пожертвовать почку только для близких, но не могут из-за несовместимости по группе крови или другим факторам, и алгоритм Гэйла — Шепли помог через сложные цепочки обмена сводить такие пары друг с другом.
Источник: Tproger / Алгоритмы спасают людей: как алгоритм подбора пар сохраняет жизни

Где живут люди, в языке которых нет числительных?
В языке индейского народа пирахан из бразильских джунглей нет числительных. Они могут лишь сказать «немножко», «побольше» и «много», то есть не способны средствами языка чётко отличить даже один предмет от пары. Исследователь Дэниел Эверетт несколько месяцев пытался научить их считать до десяти или складывать хотя бы 1+1, но не смог этого сделать. Не существует у пирахан и названий цветов, а только описательные фразы, например, «как кровь» для красного.
Источник: Wikipedia / Pirahã language

Какое число названо в честь демона?
Одно из простых чисел, 1 000 000 000 000 066 600 000 000 000 001, названо в честь демона Бельфегора, который потворствует лени, снабжая людей гениальными изобретениями и открытиями. У него много интересных свойств: это число-палиндром, в его центре находится число зверя 666, с каждой стороны шестёрки обрамлены тринадцатью нулями. Обозначают число Бельфегора обычно перевёрнутой буквой π.
Источник: Википедия / Простое число Бельфегора

Почему некоторые открытия Эйлера названы именами других учёных?
Леонард Эйлер сделал огромное множество открытий. В его честь названо большое количество физических и математических объектов, причём не по одному разу: существует несколько формул Эйлера, уравнений Эйлера, теорем Эйлера, чисел Эйлера. Чтобы избежать слишком сильной многозначности, некоторые подобные открытия и теоремы названы в честь учёных, которые совершили или доказали их первыми после Эйлера.
Источник: Wikipedia / List of things named after Leonhard Euler

За сколько ходов можно собрать кубик Рубика из любой позиции?
Стандартный кубик Рубика можно собрать из любой позиции не более чем за 20 ходов. Математическое обоснование этого получило название алгоритм Бога, а максимальное количество ходов в таком алгоритме — число Бога. Аналогичные числа можно высчитать и для других перестановочных головоломок: например, пятнашки могут быть решены за 80 ходов.
Источник: Википедия / Алгоритм Бога
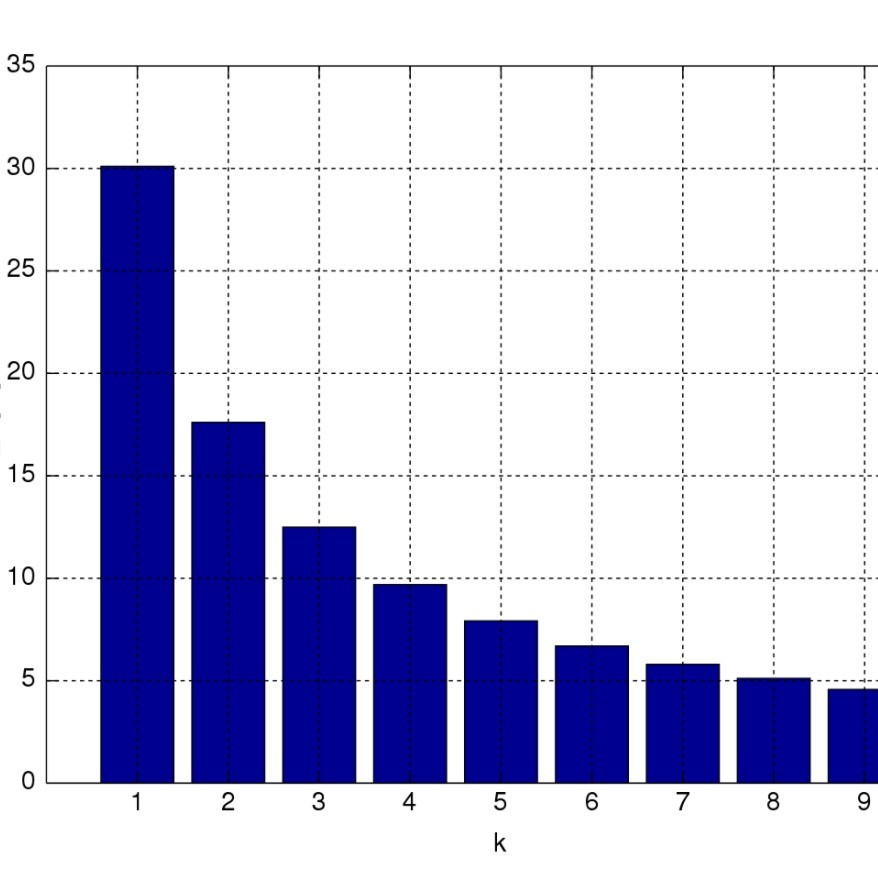
Какой закон распределения цифр позволяет проверять на достоверность финансовые данные?
Существует математический закон Бенфорда, который гласит, что распределение первых цифр в числах каких-либо наборов данных из реального мира неравномерно. Цифры от 1 до 4 в таких наборах (а именно статистика рождаемости или смертности, номера домов и т.п.) на первой позиции встречаются гораздо чаще, чем цифры от 5 до 9. Практическое применение этого закона заключается в том, что по нему можно проверять на достоверность бухгалтерские и финансовые данные, результаты выборов и многое другое. В некоторых штатах США несоответствие данных закону Бенфорда даже является формальной уликой в суде.
Источник: Wikipedia / Benford's law
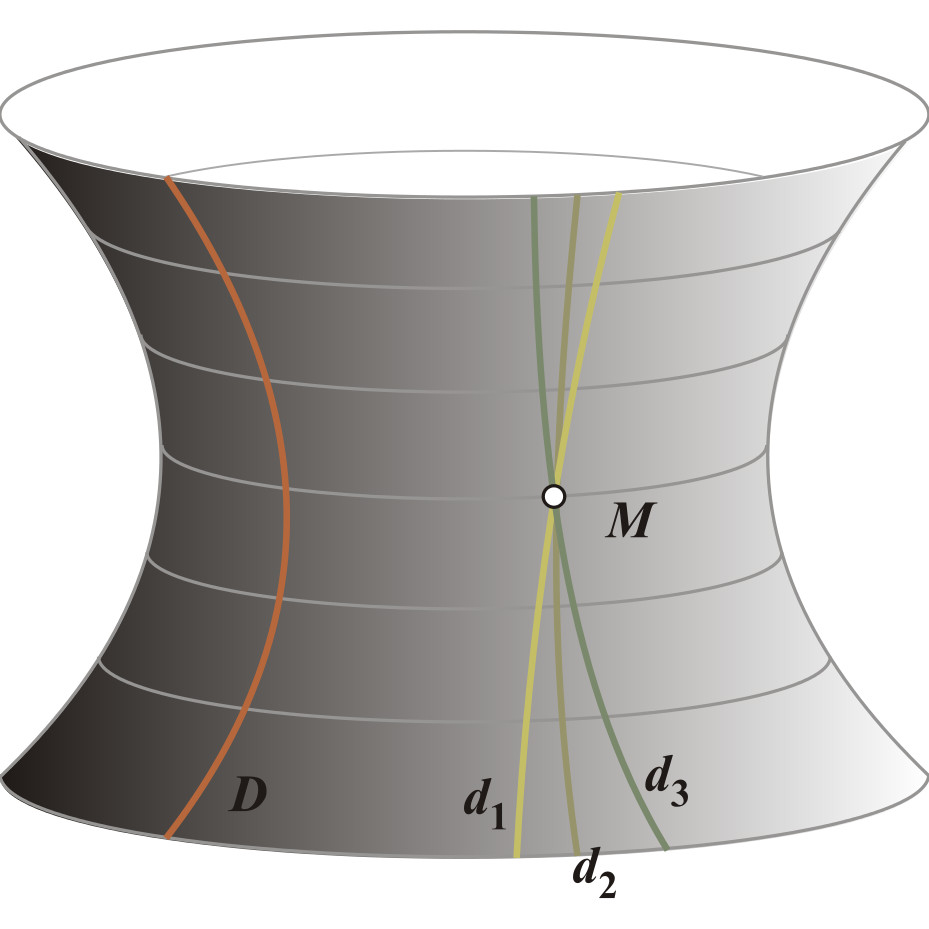
Что происходит с параллельными прямыми в геометрии Лобачевского?
По распространённому мнению, в геометрии Лобачевского параллельные прямые пересекаются. На самом деле, они не могут пересекаться ни в какой геометрии в силу самого определения параллельности. Главным же отличием геометрии Лобачевского от евклидовой является то, что через точку, не лежащую на данной прямой, можно провести не одну, а по крайней мере две не пересекающих её прямых, находящихся в той же плоскости.
Источник: Википедия / Геометрия Лобачевского

Кому в институте выдали рекомендательное письмо со строчкой: «Он — гений математики»?
Одно из самых лаконичных рекомендательных писем для поступления в университет получил математик Джон Нэш, прототип героя фильма «Игры разума». Помимо шаблонных фраз, его институтский преподаватель написал только одну фразу: «Он — гений математики».
Источник: Википедия / Нэш, Джон Форбс

Какая рекламная кампания провалилась из-за математической неграмотности американцев?
В начале 1980-х годов сеть ресторанов быстрого питания A&W запустила масштабную рекламную кампанию своего гамбургера. В отличие от похожего сэндвича с порцией мяса в 1/4 фунта из McDonald's, гамбургер A&W содержал 1/3 фунта мяса и стоил чуть дешевле, а покупатели говорили, что он вкуснее. Несмотря на всё это, кампания провалилась. Позже A&W провела исследование и выявила причину: многие клиенты не понимали истинного значения дробных чисел, и предложение казалось им невыгодным, ведь 3 меньше 4. В 2021 году компания перезапустила кампанию, однако на этот раз обозначила вес бургера как 3/9 в надежде на то, что уж в этой дроби все цифры больше аналогов.
Источник: Wikipedia / A&W Restaurants

Почему в обычном школьном классе скорее всего найдутся двое, родившиеся в один день?
В группе из 23 и более человек с вероятностью более 50% найдутся двое, отмечающие день рождения в один и тот же день. В коллективе из 57 человек вероятность совпадения дней рождения составляет уже 99%.
Источник: Википедия / Парадокс дней рождения
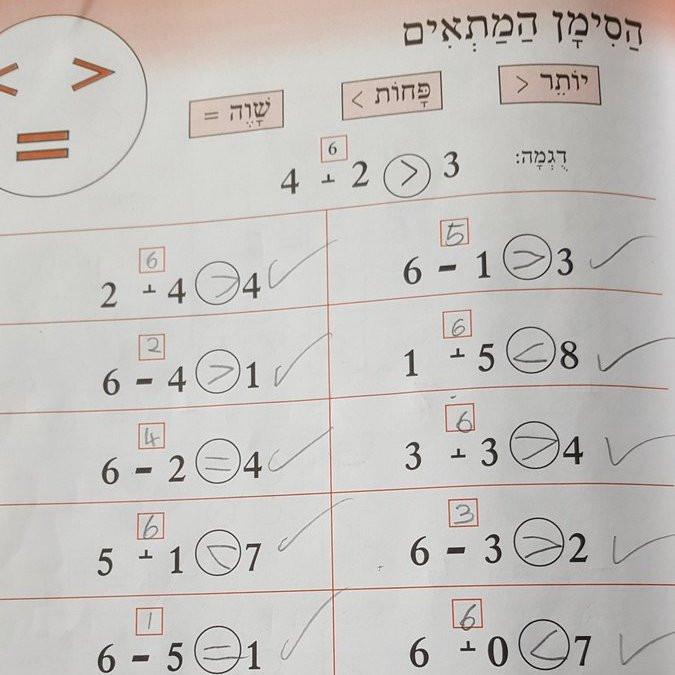
Какой знак вместо плюса используют ученики израильских школ?
Религиозные евреи стараются избегать христианской символики и вообще знаков, похожих на крест. Например, ученики некоторых израильских школ вместо плюса пишут знак ﬩, повторяющий перевёрнутую букву «т».
Источник: Wikipedia / Plus and minus signs

Какая игра связана с числом дьявола?
Сумма всех чисел на рулетке в казино равняется числу зверя — 666. Из-за этого факта рулетку иногда называют «чёртовым колесом».
Источник: Lenta.ru / Казино всегда выигрывает

Какому учёному в карьере помогли комнатные обои?
Софья Ковалевская познакомилась с математикой в раннем детстве, когда на её комнату не хватило обоев. Вместо них стены комнаты были оклеены листами с лекциями Остроградского. Когда Ковалевская брала уроки дифференциального исчисления в возрасте 15 лет, ей довольно легко давались многие понятия, так как соответствующие формулы врезались в память задолго до этого.

Зачем футболист «Интера» выступал с плюсиком между цифрами своего игрового номера?
Перейдя в 1998 году в «Интер», Роберто Баджо попросил себе любимый 10 номер. Роналдо уступил его, но потребовал майку с 9 номером, под которым выступал чилиец Иван Саморано. Тот взял номер 18, однако между единицей и восьмёркой на его форме красовался плюсик.
Источник: Wikipedia / Iván Zamorano

Какие овощи имеют соцветия в виде фракталов?
Соцветия капусты сорта романеско представляют собой фракталы. Бутоны растения описываются логарифмической спиралью и состоят из более мелких бутонов, тоже закрученных подобным образом. Эта самоподобная структура повторяется несколько раз.
Источник: Википедия / Романеско (капуста)

Чем пожертвовала Софья Ковалевская ради возможности заниматься наукой?
Чтобы получить возможность заниматься наукой, Софье Ковалевской пришлось заключить фиктивный брак и уехать из России. В то время российские университеты просто не принимали женщин, а чтобы эмигрировать, девушка должна была иметь согласие отца или мужа. Так как отец Софьи был категорически против, она вышла замуж за молодого учёного Владимира Ковалевского. Хотя в итоге их брак стал фактическим, и у них родилась дочь.

Кто и когда выиграл джек-пот лотереи, просто перебрав все возможные комбинации чисел?
В феврале 1992 года состоялся розыгрыш лотереи Виргинии «6 из 44», где джек-пот составлял 27 миллионов долларов. Число всех возможных комбинаций в таком виде лотереи было чуть выше 7 миллионов, а каждый билет стоил 1 доллар. Предприимчивые люди из Австралии создали фонд, собрав по 3 тысячи долларов от 2500 человек, купили нужное число бланков и вручную заполнили их различными комбинациями цифр, получив после выплаты налогов тройную прибыль.
Источник: The New York Times / Lottery Investors Unsure If Jackpot Was Virginia's

Когда празднуют день числа π?
У числа π есть два неофициальных праздника. Первый — 14 марта, потому что этот день в Америке записывается как 3.14. Второй — 22 июля, которое в европейском формате записывается как 22/7, а значение такой дроби является достаточно популярным приближённым значением числа π.
Источник: Википедия / День числа пи

Где и когда пытались законодательно округлить число π?
В штате Индиана в 1897 году был выпущен билль, законодательно устанавливающий значение числа π равным 3,2. Законопроект был принят Палатой представителей, но благодаря своевременному вмешательству профессора университета не прошёл голосование в Сенате штата.
Источник: Википедия / Законопроект о числе Пи

Кто стал профессором математики, не имея математического образования после средней школы?
Стивен Хокинг — один из крупнейших физиков-теоретиков и популяризатор науки. В рассказе о себе Хокинг упомянул, что стал профессором математики, не получая никакого математического образования со времён средней школы. Когда Хокинг начал преподавать математику в Оксфорде, он читал учебник, опережая собственных студентов на две недели.
Источник: Википедия / Хокинг, Стивен Уильям

Какое направление мысленной числовой линии является врождённым?
Взрослые люди располагают числа по возрастанию на мысленной числовой линии так, как привыкли писать: мы — слева направо, а, например, арабы — справа налево. Однако эксперименты с ещё не владеющими письмом младенцами показывают, что врождённое представление об ориентации числовой оси — всё-таки слева направо. Более того, эта же ориентация, видимо, свойственна и для других животных. Маленьких цыплят научили находить пищу за экраном с 5 квадратиками, а потом предлагали два других одинаковых экрана. Если на них было по 2 квадрата, большинство цыплят шли к левому экрану, а если по 8 — к правому, и результаты эксперимента подтвердились также для чисел 20, 8 и 32.
Источник: Элементы / У цыплят, как и у людей, мысленная числовая линия идет слева направо
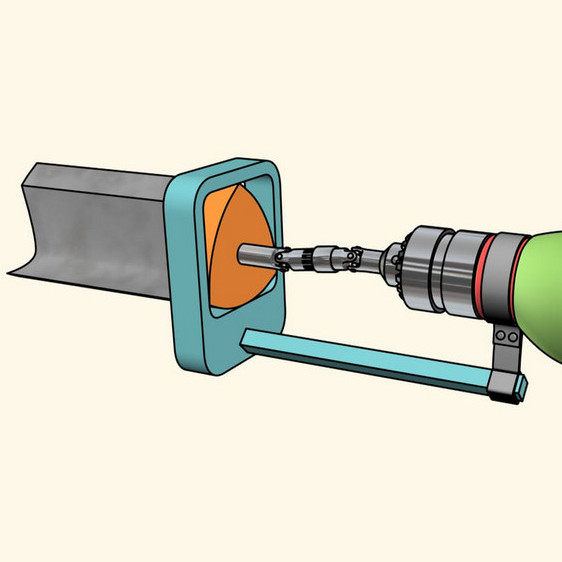
Каким сверлом можно просверлить квадратное отверстие?
Треугольник Рёло — это геометрическая фигура, образованная пересечением трёх равных кругов некоего радиуса с центрами в вершинах равностороннего треугольника со стороной, равной этому радиусу. Сверло, сделанное на основе треугольника Рёло, позволяет сверлить квадратные отверстия (с неточностью примерно в 2%).
Источник: Википедия / Кривая постоянной ширины

Какое множество чисел равняется единице в Великобритании в юридическом смысле?
В Великобритании в юридическом смысле к единице отнесены все числа, большие 0,5 и меньшие 1,5. Поводом для такого решения стало судебное разбирательство между двумя фармацевтическими компаниями. Одна из них владеет патентом на средство для заживления ран с содержанием ионов серебра от 1 до 25% массы лекарства, а другая выпустила подобное средство, которое включает 0,77% таких ионов. Ранее в подобных случаях за единицу принимались числа, большие 0,95, однако суд при рассмотрении дела обнаружил асимметрию в определении, постановил считать единицей всё в интервале от 0,5 до 1,5 и тем самым удовлетворил иск о нарушении патента.
Источник: N+1 / Суд Великобритании дал новое определение числу «1»

Какова вероятность получения одинаковых колод карт после перемешивания?
Каждый раз, когда вы перемешиваете колоду, вы создаёте последовательность карт, которая с очень высокой степенью вероятности никогда не существовала во Вселенной. Количество комбинаций в стандартной игральной колоде равно 52!, или 8×1067. Чтобы достичь хотя бы 50% вероятности получить комбинацию второй раз, нужно сделать 9×1033 перемешиваний. А если гипотетически заставить всё население планеты за последние 500 лет непрерывно мешать карты и каждую секунду получать новую колоду, в итоге получится не более 1020 разных последовательностей.
Источник: Now I Know / Shuffled

Почему возникла десятичная система счисления?
Используемая нами десятичная система счисления возникла по причине того, что у человека на руках 10 пальцев. Способность к абстрактному счёту появилась у людей не сразу, а использовать для счёта именно пальцы оказалось удобнее всего. Цивилизация майя и независимо от них чукчи исторически использовали двадцатичную систему счисления, применяя пальцы не только рук, но и ног. В основе распространённых в Шумере и Вавилоне двенадцатеричной и шестидесятеричной систем тоже было использование рук: большим пальцем отсчитывались фаланги других пальцев ладони, число которых равно 12.
Источник: Википедия / Пальцевый счет

Какова вероятность выигрыша в пасьянсе «Свободная ячейка»?
Первая версия пасьянса «Свободная ячейка» от Microsoft содержала 32 000 раскладов, а в справке было указано: «Считается (хотя и не доказано), что данный пасьянс сходится при любом раскладе». В специальном интернет-сообществе игроки делились решениями, и ни одному из них не покорился расклад № 11982. Позже математически было доказано, что для него действительно нет решения. А всего вероятность выпадения решаемой комбинации карт в этом пасьянсе оценивается более чем в 99,99%.
Источник: Википедия / Свободная ячейка

Какой последовательностью описывается расположение листьев на ветках растений?
Листья на ветке растения всегда располагаются в строгом порядке, отстоя друг от друга на определённый угол по часовой стрелке или против неё. Величина угла разная у различных растений, но её всегда можно описать дробью, в числителе и знаменателе которой — числа из ряда Фибоначчи. Например, у бука этот угол равен 1/3, или 120°, у дуба и абрикоса — 2/5, у груши и тополя — 3/8, у ивы и миндаля — 5/13 и т.д. Такое расположение позволяет листьям наиболее эффективно получать влагу и солнечный свет.
Источник: Wikipedia / Phyllotaxis
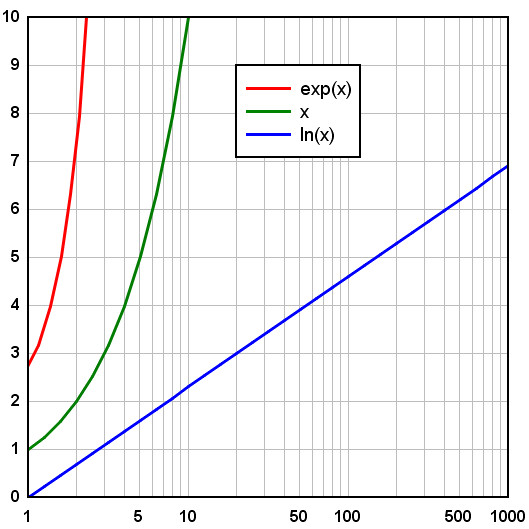
Какой способ расположения чисел на числовой оси является интуитивным для человека?
Расположение чисел на числовой оси равномерно — это приобретённая способность человека, обусловленная воспитанием и образованием, в то время как врождённо-интуитивным подходом является расположение чисел по логарифмической шкале. Такие выводы сделаны на основании работы с индейцами племени мундуруку, жившими в бассейне Амазонки, большинство из которых не имело никакого образования. Им показывали некоторое количество точек или проигрывали несколько одинаковых звуков, а затем просили показать это число на оси от 1 до 10 или от 10 до 100. Чем меньше было число, тем больше пространства отводили для него испытуемые, что как раз соответствует логарифмической шкале. Сходные результаты демонстрировали и маленькие дети из США, ещё не умевшие считать, а вот взрослые американцы и образованные мундуруку были склонны располагать числа более равномерно.

Кто и за что удостаивается Шнобелевской премии?
В начале октября каждого года, когда называются лауреаты Нобелевской премии, параллельно происходит вручение пародийной Шнобелевской премии (Ig Nobel Prize) за достижения, которые сначала заставляют засмеяться, а потом — задуматься. В 2009 году среди лауреатов были ветеринары, которые доказали, что корова, имеющая какую бы то ни было кличку, даёт больше молока, чем безымянная. Премия по литературе досталась ирландской полиции за выписывание пятидесяти дорожных штрафов некоему Prawo Jazdy, что по-польски означает «водительское удостоверение». А в 2002 году «Газпром» оказался в списке компаний, удостоенных премии по экономике за применение математической концепции мнимых чисел в сфере бизнеса.
Источник: Википедия / Шнобелевская премия

Какой математик сделал из своего имени фрактал?
Создатель фрактальной геометрии и самого понятия «фрактал» Бенуа Мандельброт часто подписывался как Benoit B. Mandelbrot, хотя от рождения у него не было среднего имени. Полагают, что математик задумал расшифровку сокращения B. как Benoit B. Mandelbrot, то есть превратил своё собственное имя в бесконечный фрактал.
Источник: Wikipedia / Benoit Mandelbrot, Wired / Never Trend Away: Jonathan Coulton on Benoit Mandelbrot

Как связаны между собой шахматы, пшеница и разорение?
Известно много притч о том, как один человек предлагает другому расплатиться с ним за некоторую услугу следующим образом: на первую клетку шахматной доски тот положит одно зёрнышко, на вторую — два и так далее. То есть на каждой следующей клетке зёрен окажется вдвое больше, чем на предыдущей. В результате тот, кто расплачивается таким образом, непременно разоряется. Это неудивительно: если зёрна пшеничные, то их общий вес составит 1,2 триллиона тонн — это больше, чем собранный урожай пшеницы за всю историю человечества.

Почему инженеров советского завода лишили премий за оптимизацию раскроя стальных листов?
Леонид Канторович, единственный отечественный обладатель Нобелевской премии по экономике, предложил метод оптимизации распила фанеры, который в 1949 году инженеры Ленинградского вагоностроительного завода применили к раскрою стальных листов и улучшили показатели. Однако так как вместо теоретического увеличения выпуска на 4% прирост на практике составил только 2,5%, сотрудников лишили премий. Другой причиной для наказания стало невыполнение заводом плана по сдаче металлолома из-за снижения количества обрезков. Стоит заметить, что из-за поднятой шумихи инженерам всё же выплатили премии, а метод оптимизации внедрили в широкую практику.

Какому правилу, выведенному Леонардо, подчиняются ствол и ветви деревьев?
Леонардо да Винчи вывел правило, согласно которому квадрат диаметра ствола дерева равен сумме квадратов диаметров ветвей, взятых на общей фиксированной высоте. Более поздние исследования подтвердили его с одним лишь отличием — степень в формуле необязательно равняется 2, а лежит в пределах от 1,8 до 2,3. Традиционно считалось, что эта закономерность объясняется тем, что у дерева с такой структурой оптимальный механизм снабжения веток питательными веществами. Однако в 2010 году американский физик Кристоф Эллой нашёл более простое механическое объяснение феномену: если рассматривать дерево как фрактал, то закон Леонардо минимизирует вероятность слома веток под воздействием ветра.
Источник: Lenta.ru / Фракталы связали правило Леонардо с напором ветра

Какие насекомые способны разговаривать и выполнять простейшие арифметические действия?
Отдельные высокосоциальные виды муравьёв способны объяснять друг другу путь к пище, умеют считать и выполнять простейшие арифметические действия. Например, когда муравей-разведчик находит еду в специально сконструированном лабиринте, он возвращается и движениями антенн и ног объясняет, как пройти к ней, другим муравьям. Если в это время заменить лабиринт на аналогичный, то есть убрать феромоновый след, сородичи разведчика всё равно найдут пищу. В другом эксперименте разведчик ищет в лабиринте из многих одинаковых ответвлений, и после его объяснений другие насекомые сразу бегут к обозначенному ответвлению. А если сначала приучить разведчика к тому, что пища с большей вероятностью будет находиться в 10-м, 20-м и так далее ответвлениях, муравьи принимают их за базовые и начинают ориентироваться, прибавляя или отнимая от них нужное число, то есть используют систему, аналогичную римским цифрам.
Источник: Коммерсантъ / Муравьи считают лучше британских пятиклассников

Какой советский лозунг стал прообразом знаменитой фразы Джорджа Оруэлла?
Знаменитая формула «Дважды два равняется пяти» наиболее известна по антиутопии Оруэлла «1984». Писатель позаимствовал её из названия главы книги Юджина Лайонса о поездке в СССР, где тот услышал лозунг «Пятилетку — в четыре года!». Формулу употребляли и другие писатели, например, Достоевский в «Записках из подполья», хотя и в другом смысле. Главный герой не принимает мир с жёстко установленными правилами и говорит, что «дважды два пять — премилая иногда вещичка».
Источник: Википедия / Дважды два — пять

Какой математик вычислил по формуле день своей смерти?
Английский математик Абрахам де Муавр в престарелом возрасте однажды обнаружил, что продолжительность его сна растёт на 15 минут в день. Составив арифметическую прогрессию, он определил дату, когда она достигла бы 24 часов — 27 ноября 1754 года. В этот день он и умер.
Источник: Wikipedia / Abraham de Moivre
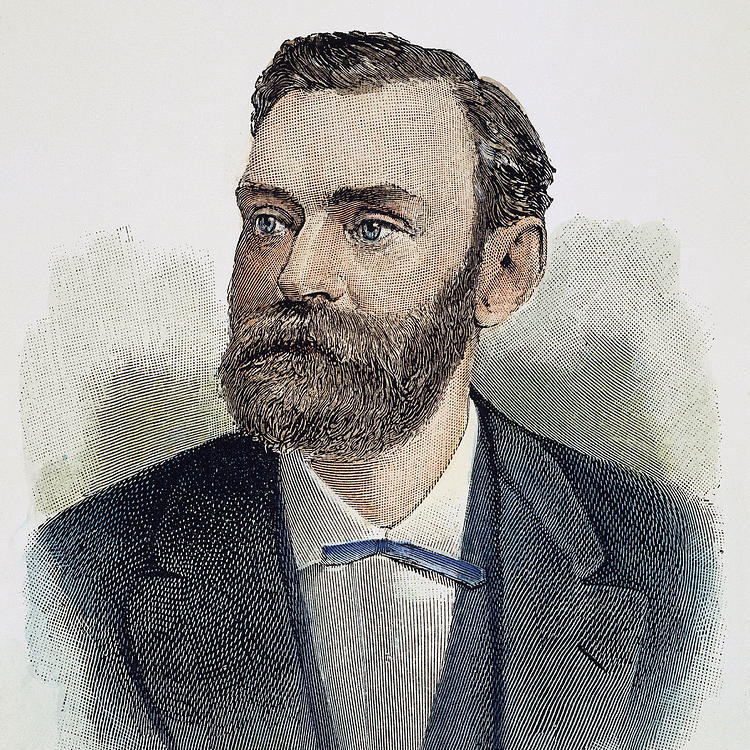
Почему Нобелевская премия не вручается за достижения в математике?
Бытует мнение, что Альфред Нобель не включил математику в список дисциплин своей премии из-за того, что его жена изменила ему с математиком. На самом деле Нобель никогда не был женат. Настоящая причина игнорирования математики Нобелем неизвестна, но есть несколько предположений. Согласно одному из них, на тот момент уже существовала премия по математике от шведского короля. Согласно другому, математики не делают важных изобретений для человечества, так как эта наука имеет чисто теоретический характер.
Источник: Snopes / No Nobel Prize for Math

Картины какого художника соответствуют математическому описанию турбулентных потоков?
Математики, исследовавшие картины Ван Гога, пришли к выводу, что завихрения на некоторых его полотнах довольно точно описывают невидимые для глаза турбулентные потоки воздуха. Это выражается в том, что большая или меньшая яркость точек на картинах пропорциональна скоростям точек потока в соответствующих координатах при математическом моделировании турбулентности. Учёные также отмечают, что подобные картины, в том числе знаменитая «Звёздная ночь», писались Ван Гогом в периоды психической нестабильности.
Источник: Газета.ru / Ван Гог математически точно изображал турбулентные потоки
Кто решил сложную математическую проблему, приняв её за домашнее задание?
Американский математик Джордж Данциг, будучи аспирантом университета, однажды опоздал на урок и принял написанные на доске уравнения за домашнее задание. Оно показалось ему сложнее обычного, но через несколько дней он смог его выполнить. Оказалось, что он решил две «нерешаемые» проблемы в статистике, над которыми бились многие учёные.
Источник: Wikipedia / George Dantzig

При каких обстоятельствах «Мудрец из Страны Оз» превратился в «Волшебника Изумрудного города»?
В конце 1930-х годов Александр Волков, который по образованию был математиком и преподавал эту науку в одном из московских институтов, стал изучать английский язык и для практики решил перевести сказку «Мудрец из Страны Оз» американского писателя Фрэнка Баума. Сыновьям Волкова сказка понравилась, они стали требовать продолжения, и Волков помимо перевода начал придумывать что-то от себя. Так появился «Волшебник Изумрудного города» и другие книги о Волшебной стране. А «Мудрец из страны Оз» в простом переводе на русский не издавался до 1991 года.
Источник: Википедия / Волков, Александр Мелентьевич, Изумрудный город / Волков Александр Мелентьевич
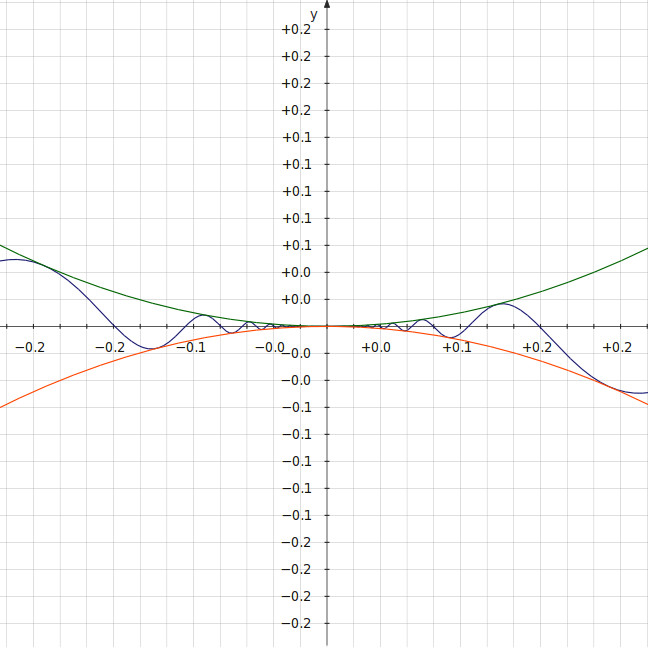
Какой математический закон раскрывается в теореме о двух милиционерах?
Некоторые математические законы называют по аналогии с ситуациями в реальной жизни. Например, теорема о существовании предела у функции, которая «зажата» между двумя другими функциями, имеющими одинаковый предел, называется теоремой о двух милиционерах. Это объясняется тем, что если два милиционера держат между собой преступника и при этом идут в камеру, то заключённый также вынужден туда идти.
Источник: Википедия / Теорема о двух милиционерах

На защите чьей диссертации присутствовало больше футбольных болельщиков, чем учёных?
Знаменитый датский физик Нильс Бор увлекался футболом и был вратарём клуба «Академиск». Его брат Харальд также был доктором наук — он специализировался в математике — и выступал в том же клубе, но привлекался ещё и в сборную Дании. Харальд Бор был настолько популярен у публики, что на защите его диссертации присутствовало больше футбольных болельщиков, чем математиков.
Источник: Wikipedia / Harald Bohr

Какие оценки по математике получал Эйнштейн в школе?
Во многих источниках, зачастую с целью ободрения плохо успевающих учеников, встречается утверждение, что Эйнштейн завалил в школе математику или, более того, вообще учился из рук вон плохо по всем предметам. На самом деле всё обстояло не так: Альберт ещё в раннем возрасте начал проявлять талант в математике и знал её далеко за пределами школьной программы. Позднее Эйнштейн не смог поступить в Швейцарскую высшую политехническую школу Цюриха, показав высшие результаты по физике и математике, но не добрав нужное количество баллов в других дисциплинах. Подтянув эти предметы, он через год в возрасте 17 лет стал студентом данного заведения.
Источник: Wikipedia / Albert Einstein